Multy armed bandits
Теги: machine-learning r-learning
k-рукие бандиты решают следующую задачу: есть k вариантов действий, мы многократно стоим перед проблемой выбора из этих вариантов. После каждого выбора мы получаем численное вознаграждение, выбираемое из стационарного распределения вероятностей, которое зависит от выбранного действия. Цель - максимизировать ожидаемое полное вознаграждение за определенный период. Благодаря повторному выбору, мы стремимся максимизировать выбор только лучших решений. Ценность произвольного действия a:
\[q_*(a) \doteq \mathbb{E}[R_t|A_t = a]\]где \(A_t\) действие, выбранное на шаге t, а \(R_t\) соответствующее ему вознаграждение. На практике ценность каждого действия мы не знаем, поэтому приходится применять методы оценивания ценности действий. Если мы совершаем действия и оцениваем их, тогда на любом временном отрезке мы будем иметь максимально ценное действие или “жадное”. Когда мы выбираем жадное действие, то используем текущие знания о ценности действий, а когда выбираем какое-то другое - исследуем нежадные действия.
Истинная ценность действия - это среднее вознаграждение при условии выбора этого действия. Простейшее правило - выбирать одно из жадных действий:
\[A_t \doteq argmax_a Q_t(a)\]где \(Q_t(a)\) истинная ценность.
Альтернативный вариант - большую часть времени выбирать жадное действие, но иногда - исследовать. Методы, которые используют данный подход, называются \(\varepsilon\)-жадными. В пределе такие методы приводят к тому, что каждое действие (не только жадные), будут выбраны бесконечное число раз, что сведет истинную ценность к ценности \(q_*(a)\).
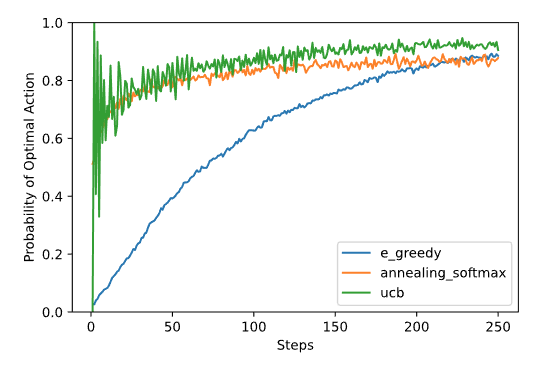
Эпислон-жадные алгоритмы зависят от выбора параметра, т.е. от предпочтения разведывать или эксплуатировать. Можно опираться на текущую оценку распределения вознаграждений (softmax), чтобы исследовать не произвольное состояние, а состоянии в направлении максимизации вознаграждения. Еще используют стратегию “отжига” \(\varepsilon\) - в начале \(\varepsilon\) большой, что провоцирует больше исследований, но к концу обучения параметр постепенно снижается, что уменьшает разведывающую способность алгоритма. Другой вариант - поощрять исследования состояний, которые ранее не посещались (это методы с верхним доверительным интервалом, upper-confidence bound, UCB). UCB полезны, т.к. у них нет гиперпараметров. Ниже приведено сравнение для простейшей задачи обучения с подкреплением:
Смотри еще: