Stock basic statistics
Теги: market-stocks
Базовые статистики [market-stocks]
Order book
Двусторонний стек из заявок на покупку и продажу. Слева представлены биды (заявки на покупку), справа оферы (предложения на продажу)
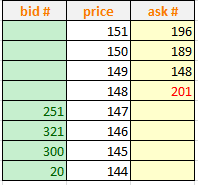
Когда появляются совпадающие заявки, происходит гарантированная сделка
Order book statistics
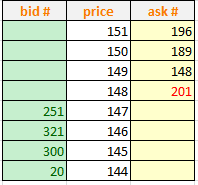
bid/ask spread:
\[BidAskSpread = BestOffer/BestBid -1\]Например здесь:
BidAskSpread = 148/147 - 1 = 0.0068…
Weighted averaged price:
$P_{VWAP}$ Volume Weighted Average Price (средневзвешенная по объему цена);
$P_{j}P_{j}$ is price of trade $jj$ (цена сделки);
$Q_{j}Q_{j}$ is quantity of trade jj$ (количество лотов);
$jj$ это каждая отдельная сделка за выбранный период, исключая кросс-трейды и кросс-трейды корзины
В данном контексте $WAP$ опреден так:
\[WAP = \frac{BidPrice_{1}*AskSize_{1} + AskPrice_{1}*BidSize_{1}}{BidSize_{1} + AskSize_{1}}\]Если в двух стаканах есть предложения спроса и предложения на одном и том же уровне цен соответственно, у стакана с большим количеством предложений будет более низкая оценка акций, поскольку в стакане больше предполагаемых продавцов, а большее количество продавцов подразумевает факт увеличения предложения на рынке, что приводит к снижению стоимости акций.
В большинстве случаев в часы непрерывной торговли в книге заказов не должно быть сценария, когда заявка на покупку выше, чем предложение продажи. Другими словами, скорее всего, спрос и предложение никогда не должны пересекаться.
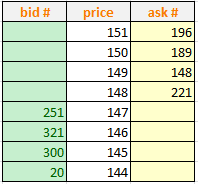
В примере выше:
$WAP$ = (177251 + 148251)/(251 + 221) = 156.875
Log returns
Как сравнить прайсы за вчера и сегодня?
Простейший метод - посчитать разницу price differences. Однако простая разница не показывает степень изменеения цены. Эту проблему можнор решить, разделив разницу на стартовую цену за выбранный период - это называется stock return. Этот показатель демонстрирует процентное изменеение цены. Stock return всегда используется в финансах, а log returns предпочтителен в математическом моделировании.
$S_t$ это рыночная цена $S$ во время $t$, определенная между временем $t_1$ и $t_2$
\[r_{t_1, t_2} = \log \left( \frac{S_{t_2}}{S_{t_1}} \right)\]Обычно kig return смотрится за фиксированный интервал, к примеру 10-тиминутный logreturn выглядит так $r_t = r_{t - 10 min, t}$.
Log returns предоставляет ряд преимуществ:
- адитивность через время $r_{t_1, t_2} + r_{t_2, t_3} = r_{t_1, t_3}$
- regular returns не может опускаться меньше -100%, в то время как log returns не ограничен
Realized volatility
При торговле опционами неплохим показателем на входе модели является стандартное отклонение от log return. Стандартное отколнение будет разным для коротких и длинных интиервалов, по этой причине это значение обычно нормализируцется к годовому периоду - это называется волатильностью volatility.
Мы можем реализовать волатильность так: посчитать log returns последовательно через все обновления order book - это будет realized volatility, $\sigma$, рассчитнаая как квадратный корень из суммы квадратов log returns. \(\sigma = \sqrt{\sum_{t}r_{t-1, t}^2}\)
Здесь мы используем WAP как рыночную цену для расчета log returns.
В данном случае нормализация к годовому периоду не делается.
В этом соревновании представлены 10-минутные book of data и необходимо предсказать волатильность в следующие 10 минут