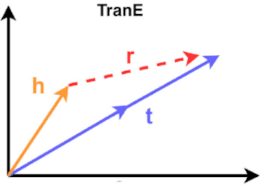
Translating алгоритмы (а точнее TransE), рассматриваются в курсе cs224w, про них есть домашка и они фигурируют в нескольких последних лекциях, есть смысл разобраться в том, как именно они устроены. Алгоритм TransE (Translating Embeddings for Modeling Multi-relational Data) осуществляет поиск эмбеддингов для нод графа с учетом их возможных связей.
Вначале сам алгоритм:

TransE использует так называемый “shallow” encoding. Каждая нода \(v\) кодируется произведением \(\mathbf{Z}*\mathbf{v}\), где \(\mathbf{Z} \in \mathbb{R}^{d * \vert v\vert}\), а \(\mathbf{v} \in \mathbb{I}^{\vert v\vert }\) (0 всюду кроме колонки , индицирующей \(v\)). Таким образом мы получаем вектора одинаковой размерности для всех нод, по одному для каждой ноды.
В задачах, решаемых TransE, мы имеем некий граф знаний \(G = (E, S, L)\), в котором \(E\) — это множество нод (entities), \(S\) — множество ребер, а \(L\) — множество возможных связей.
\(S\) содержит триплеты \((h, l, t)\), определяемые следующим образом:
\(h \in E\) — исходящая нода (head)
\(l \in L\) — связь (relation)
\(t \in E\) — нода, завершающая связь (tail)
Можно представить себе граф, в котором существуют точки, для которых сложно определить близость. Например, в графе территорий и населенных пунктов город Москва (head) является столицей России (tail). Между данными нодами графа есть некая связь (relation). Задача алгоритма TransE обучиться такому векторному представлению для \((h, l, t)\), чтобы оно отображало эту связь для всех аналогично связанных нод. Итак, необходимо представить эмббеддинги head, tail и relation в пространстве \(\in \mathbb{R}^k\) (где \(k\) - это кол-во измерений), после чего обучить алгоритм таким образом, чтобы сумма head и relation была как можно ближе к tail.
Если мы исходим из того, что \((h, l, t) \in S\) и предполагаем что \(\mathbf{h} + \mathbf{l} \approx \mathbf{t}\). Такие триплеты мы можем считать “правильными”. Тогда можно предположить существование и “неправильных” (corrupted) триплетов \((h', l, t') \in S'\), выбранных из некого \(S'_{(h, l, t)}\)в котором \(h\) или \(t\) (но не оба одновременно) заменены на случайные, входящие в \(S\).
К примеру, Берлин в нашем графе мог бы оказаться столицей России, но, к счастью, такой связи мы не наблюдаем.
Итак, функция потерь, которую будет минимизировать TransE, выглядит так:
\[\mathcal{L} = \underset{(h,l,t) \in S}\sum (\underset{(h',l,t') \in S'_{(h,l,t)}}\sum [\gamma + d(\mathbf{h} + \mathbf{l}, \mathbf{t}) - d(\mathbf{h}' + \mathbf{l}, \mathbf{t}')]_{+} )\]Нам необходимо сделать так, чтобы разница правильных и неправильных эмбеддингов (с учетом зазора \(\gamma\)) \(d_{+}\) и \(d_{-}\) (с регуляризацией по норме \(L_{1}\) или \(L_{2}\)) стремилась к нулю сверху. Для этого мы будем использовать стохастический градиентный спуск с минибатчами через все \(\mathbf{h}\), \(\mathbf{l}\) и \(\mathbf{t}\). Триплеты будем выбирать семплированием, а инициализируем всю конструкцию случайными значениями.
Что будет делать алгоритм?
-
вначале мы случайным образом инициализируем все вектора \(\mathbf{l}\) для каждого \(l \in L\) и все вектора \(\mathbf{e}\) для всех entities в графе
-
нормализуем эмбеддинги, чтобы исключить тривиальную оптимизацию по кратчайшим расстояниям
-
затем, уже в цикле, будем определять размер минибатчей и иницилизировать сеты триплетов — для каждого правильного триплета в минибатче будем получать неправильный
-
наконец будем считать лос и обновлять эмбеддинги по направлению градиента
Выглядит это примерно так: мы постепенно подтягиваем эмбеддинги нод в векторном пространстве так, чтобы они отражали связь.
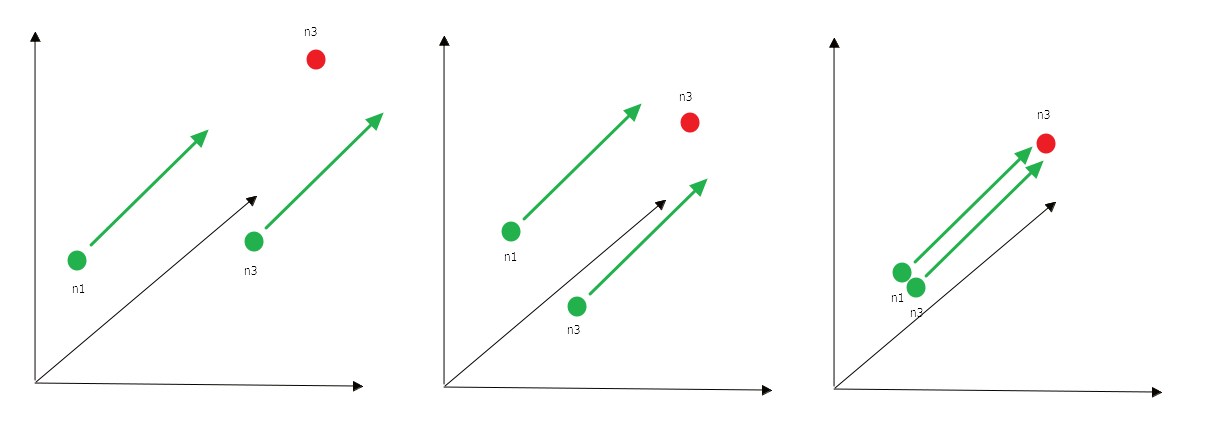
Возникает ряд вопросов. Почему бы не использовать лос попроще? Например, можно не усложнять и сводить в ноль сумму эмбеддингов всех правильных триплетов.
\[\mathcal{L}_{simple} = \underset{(h,l,t) \in S}\sum d(\mathbf{h} + \mathbf{l}, \mathbf{t})\]В этом случае может возникнуть ситуация, когда совершенно разные ноды получат одинаковые эмбеддинги. Что еще хуже — мы можем получить пустые эмбеддинги.
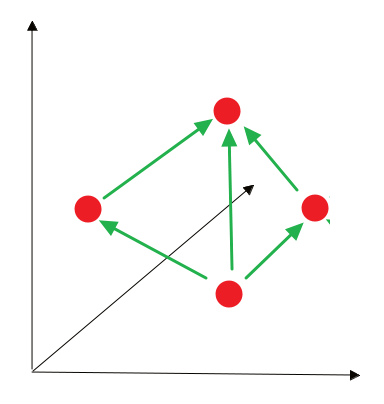
Поэтому мы оптимизируем метрику, с \((h', l, t') \in S'\). Другая проблема, которая может возникнуть — алгоритм может никогда не сойтись. Для этого нам нужен параметр \(\gamma\), который задает определенный порог, достижение которого будет считаться приемлемым в данном контексте.
Подробнее про TransE можно прочитать в статье Translating Embeddings for Modeling Multi-relational Data. Этот и другие методы для эмбеддингов на графах можно посмотреть тут, тут и тут. О том, как translating-модели применяются в совместной фильтрации в рекомендательных системах, можно посмотреть здесь.