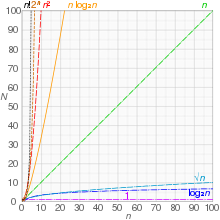
В асимптотическом анализе алгоритмов принято использовать базовые обозначения, позволяющие формализовать сложность алгоритма. Все термины сводятся к устранению постоянных коэффициентов, так как они слишком зависимы от аппаратной и программной реализации, а так же к игнорированию членов низших порядков, так как с ростом объема данных такие вычисления перестают играть значимую роль.
O-большое
Для функции, зависящей от длины \(n\) входных данных утверждается:
\(T(n) = O(f(n))\) тогда и только тогда, когда существуют положительные константы \(c\) и \(n_{0}\), такие что справедливо неравенство \(T(n) \leq c \times f(n)\) для всех \(n \geq n_{0}\). Иными словами, \(T(n)\) ограничена сверху функцией, кратной функции \(f(n)\)
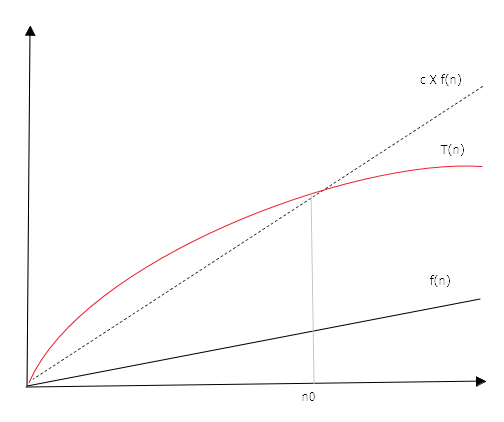
Важно: \(c\) и \(n_{0}\) не зависят от \(n\)
\(\Omega\)-большое
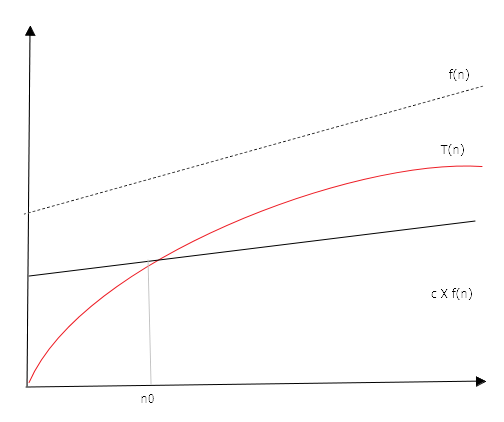
\(\Omega\) имеет тот же смысл, что и \(O\), только функция, кратная \(f(n)\) ограничивает \(T(n)\) снизу. Таким образом, две нотации реализуют наихудший и наилучший случаи. \(T(n) = \Omega(f(n))\) тогда и только тогда, когда существуют положительные константы \(c\) и \(n_{0}\), такие что справедливо неравенство \(T(n) \geq c \times f(n)\) для всех \(n \geq n_{0}\).
\(\Theta\)-большое
\(T(n) = \Theta(f(n))\) тогда и только тогда, когда существуют положительные константы \(c_{1}\), \(c_{2}\) и \(n_{0}\), такие что справедливо неравенство \(c_{1} \times f(n) \leq T(n) \geq c_{2} \times f(n)\) для всех \(n \geq n_{0}\)
o, \(\omega\), \(\theta\)-малые
Малые нотации соответствуют большим, но при условии строго неравенества.
Также читайте про временную сложность в машинном обуче6нии и про базовые принципы временной сложности